Point Pattern Basics
2/2/23
Point Pattern Basics
- Objectives & Terminology
- Examples
Objectives of Point Pattern Analysis
Point Pattern Analysis Objectives
Goals
- Pattern detection
- Assessing the presence of clustering
- Identification of individual clusters
General Approaches
- Estimate intensity of the process
- Formulating an idealized model and investigating deviations from expectations
- Formulating a stochastic model and fitting it to the data
Point Pattern Analysis Definitions
Spatial Point Pattern: A set of events, irregularly distributed within a region \(A\) and presumed to have been generated by some form of stochastic mechanism.
Representation \(\left\{Y(A), A \subset \Re \right\}\), where \(Y(A)\) is the number of events occurring in area \(A\).
Events, points, locations
- Event
-
an occurrence of interest
- Point
-
any location in study area
- Event location
-
a particular point where an event occurs
Point Pattern Analysis Definitions
Region: \(A\)
- Most often planar (two-dimensional Euclidean space)
- One dimensional applications also possible
- Three-dimensional increasingly popular (space + time)
- Point processes on networks (non-planar)
Space-Time Point Patterns
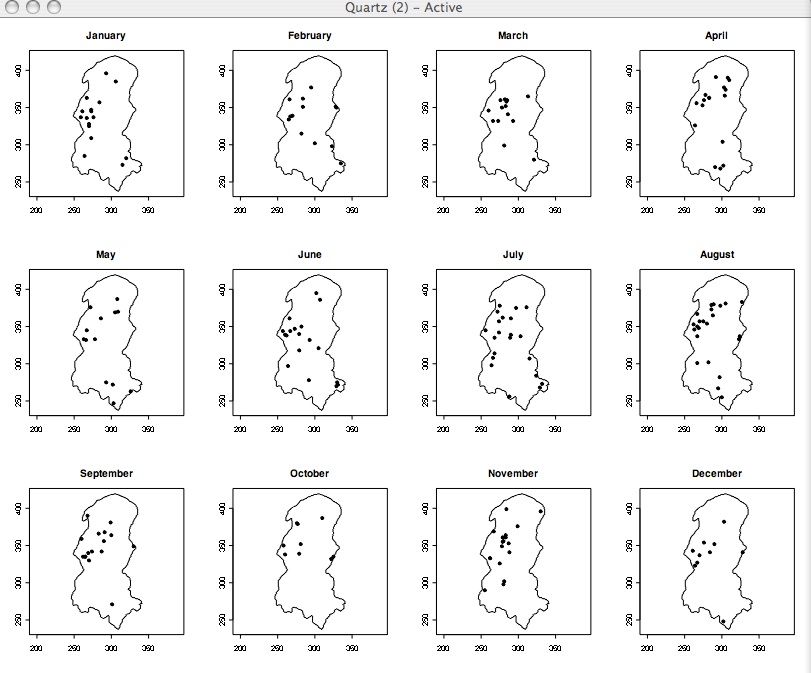
Space-Time Point Patterns
Point Patterns on Networks
Point Patterns
Unmarked Point Patterns
Only location is recorded
Attribute is binary (presence, absence)
Marked Point Patterns
Location is recorded
Non-binary stochastic attribute
e.g., sales at a retail store, dbh of tree
Realizations
Mapped Point Patterns
All events are recorded and mapped
Complete enumeration of events
Full information on the realization from the process
Sampled Point Patterns
Sample of events are recorded and mapped
Complete enumeration of events impossible or intractable
Partial information on the realization from the process
Presence/“absence” data (ecology, forestry)
Research Questions
Research Questions
Location Only are points randomly located or patterned
Location and Value
- marked point pattern
- is combination of location and value random or patterned
Both Cases: What is the Underlying Process?
Points on a Plane (Planar Point Pattern Anaysis)
Classic Point Pattern Analysis
- points on an isotropic plane
- no effect of translation and rotation
- classic examples: tree seedlings, rocks, etc
Distance
- no directional effects
- no translational effects
- straight line distance only
Events: Point Map
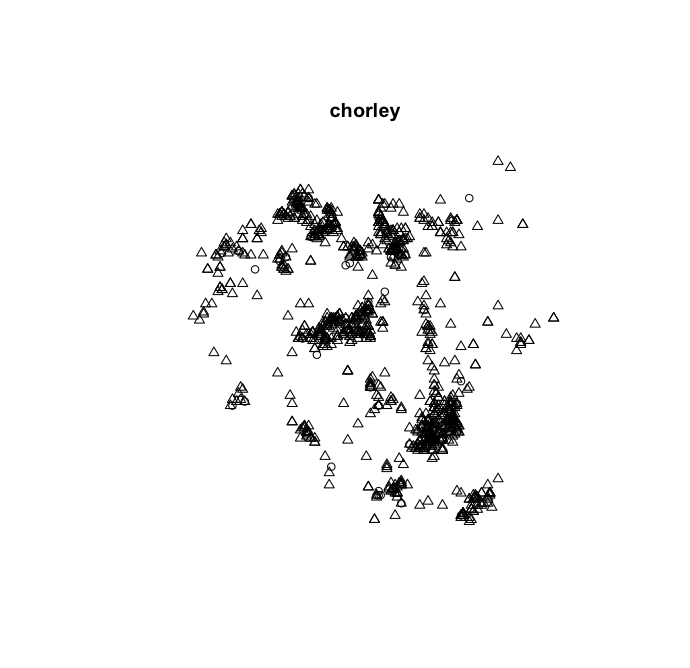
Points in Context
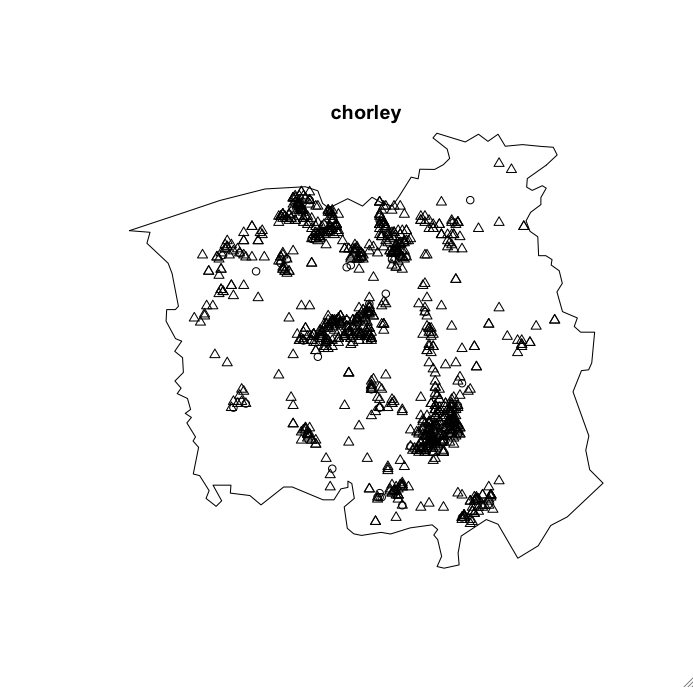
Intensity
First Moment
- number of points \(N\), area of study \(|A|\)
- intensity: \(\lambda = N/|A|\)
- area depends on bounds, often arbitrary
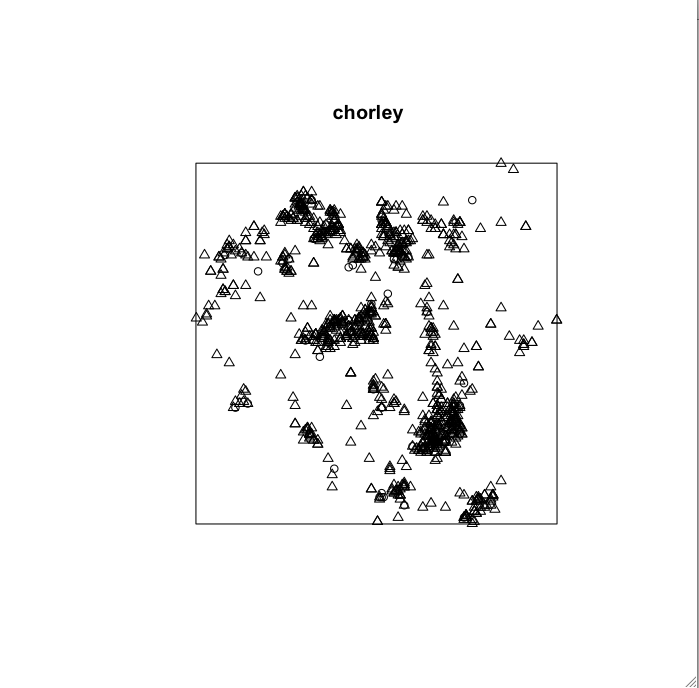
Artificial Boundaries
- bounding box (rectangle, square)
- other (city boundary)
Bounding Box
District Boundary

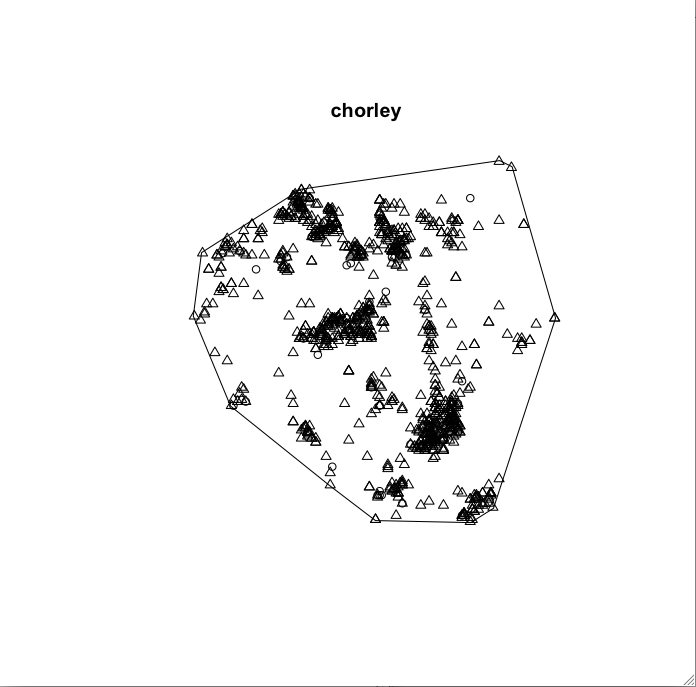
Convex Hull
Tightest fit various algorithms
Rescaled Convex Hull (Ripley-Rasson)
- adjust to properly reflect spatial domain of point process
- use centroid of convex hull
- rescale by \(1/[\sqrt{(1-m/N)}]\)
- \(m\): number of vertices of convex hull
Convex Hull
Multiple Boundaries
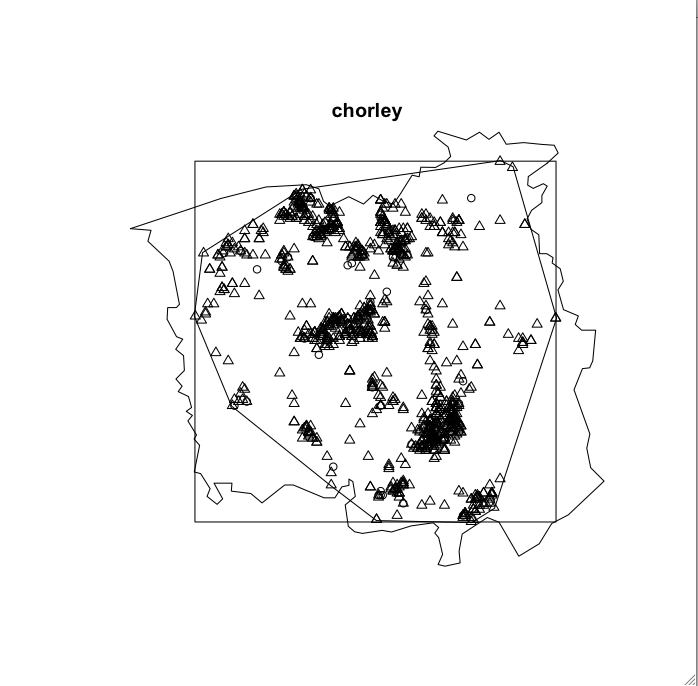
Intensity Estimates
| Area | Intensity | |
| \(km^2\) | \(cases/km^2\) | |
| District Boundary | 315.155 | 3.29 |
| Bounding Box | 310.951 | 3.33 |
| Convex Hull | 229.421 | 4.52 |
N=1036
Next Up
Centrography