Spatial Data
1/31/23
Spatial Data
- What is data?
- What is special about spatial data?
- Types of Spatial Data
What is data?
Data Definitions
facts and statistics collected together for reference or analysis
the quantities, characters, or symbols on which operations are performed by a computer, being stored and transmitted in the form of electrical signals and recorded on magnetic, optical, or mechanical recording media.
things known or assumed as facts, making the basis of reasoning or calculate
Source: Oxford languages
Data’s Place
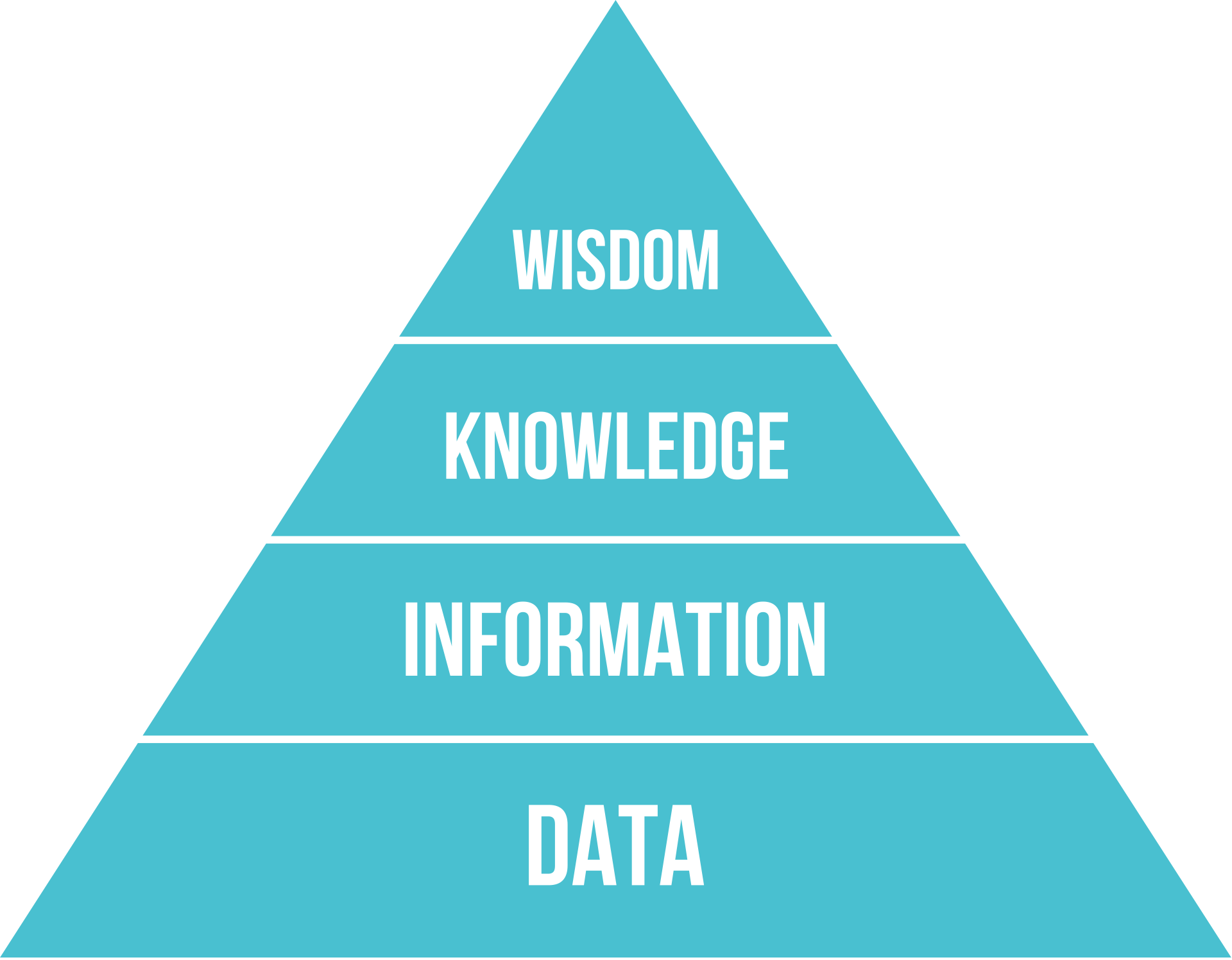
- data: discrete facts, unorganized and lacking context or information
- information: data imbued with meaning - what is in the data
- knowledge: perception of the world seen through information synthesis
- wisdom: “knowing the right things to do”
Data Sets
A data set is a collection of observations recorded for individual units on a set of variables.
Variables are sometimes referred to as attributes or features (in machine learning parlance).
Measurement Scales
| Scale | Operations | Example |
|---|---|---|
| nominal | mode, frequencies | Zip Code |
| ordinal | A > B | Ranks, Primary, Intermediate |
| interval | + - | Time |
| ratio | + - * / | Weight, Kelvin |
What is special about spatial data?
Spatial Data is Special
Spatial data comes in many varieties and it is not easy to arrive at a system of classification that is simultaneously exclusive, exhaustive, imaginative, and satisfying.
– G. Upton & B. Fingleton
What is special about spatial data?
Location, Location, Location
where matters
Dependence is the rule, not the exception
- spatial interaction, contagion, spill-overs
- spatial externalities
Spatial Scale
- Inference can change with scale
Nature of Spatial Data
Georeferences
attribute data together with location
Geocoding
- associate observations with location
- point: latitude-longtitude (GPS)
- areal unit: spatial reference
Geocoding on-line
Geocode Input
Geocoding on-line

Geocode Output
On the Map?
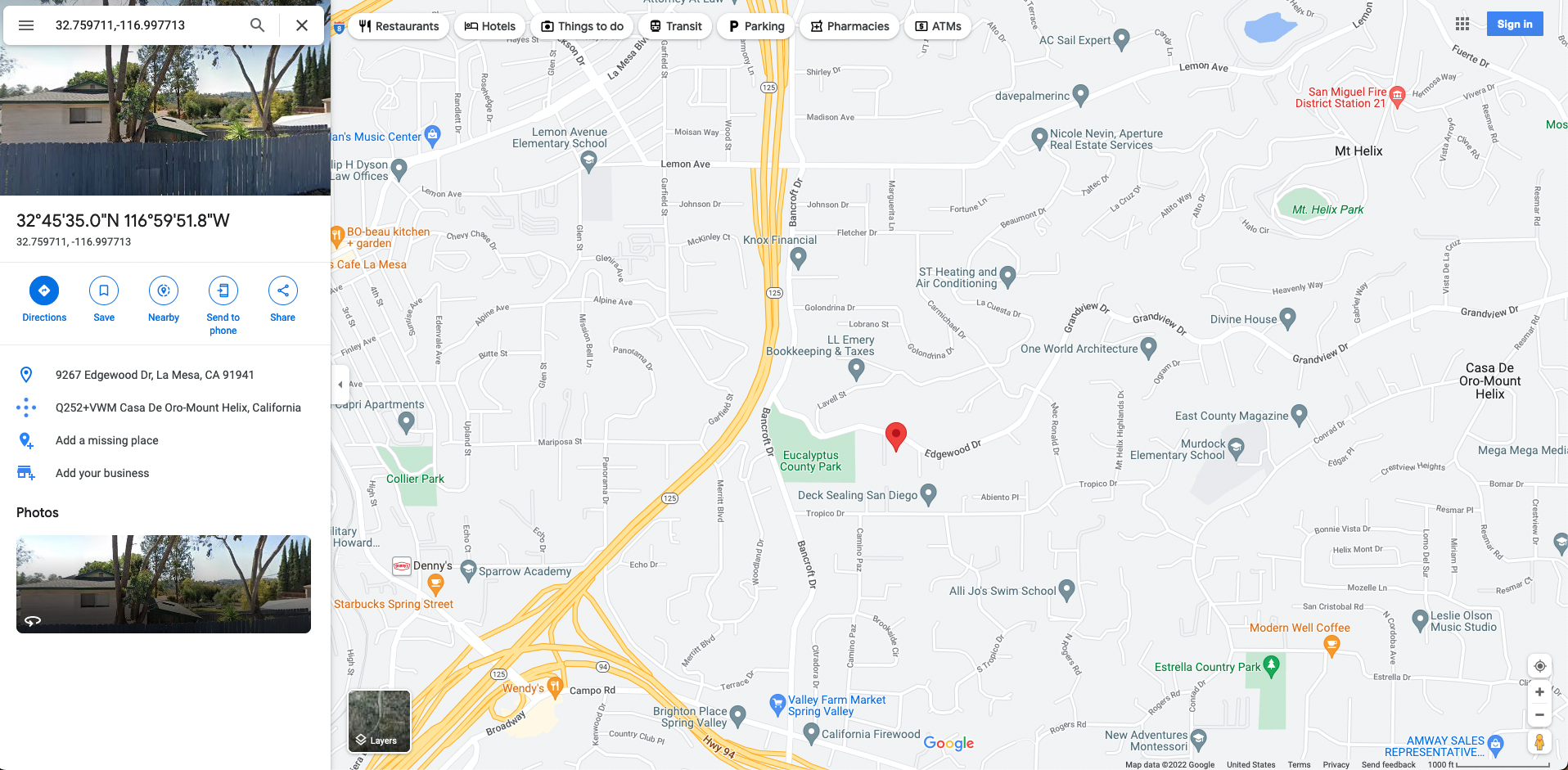
Map of Geocode Output
On the Map?
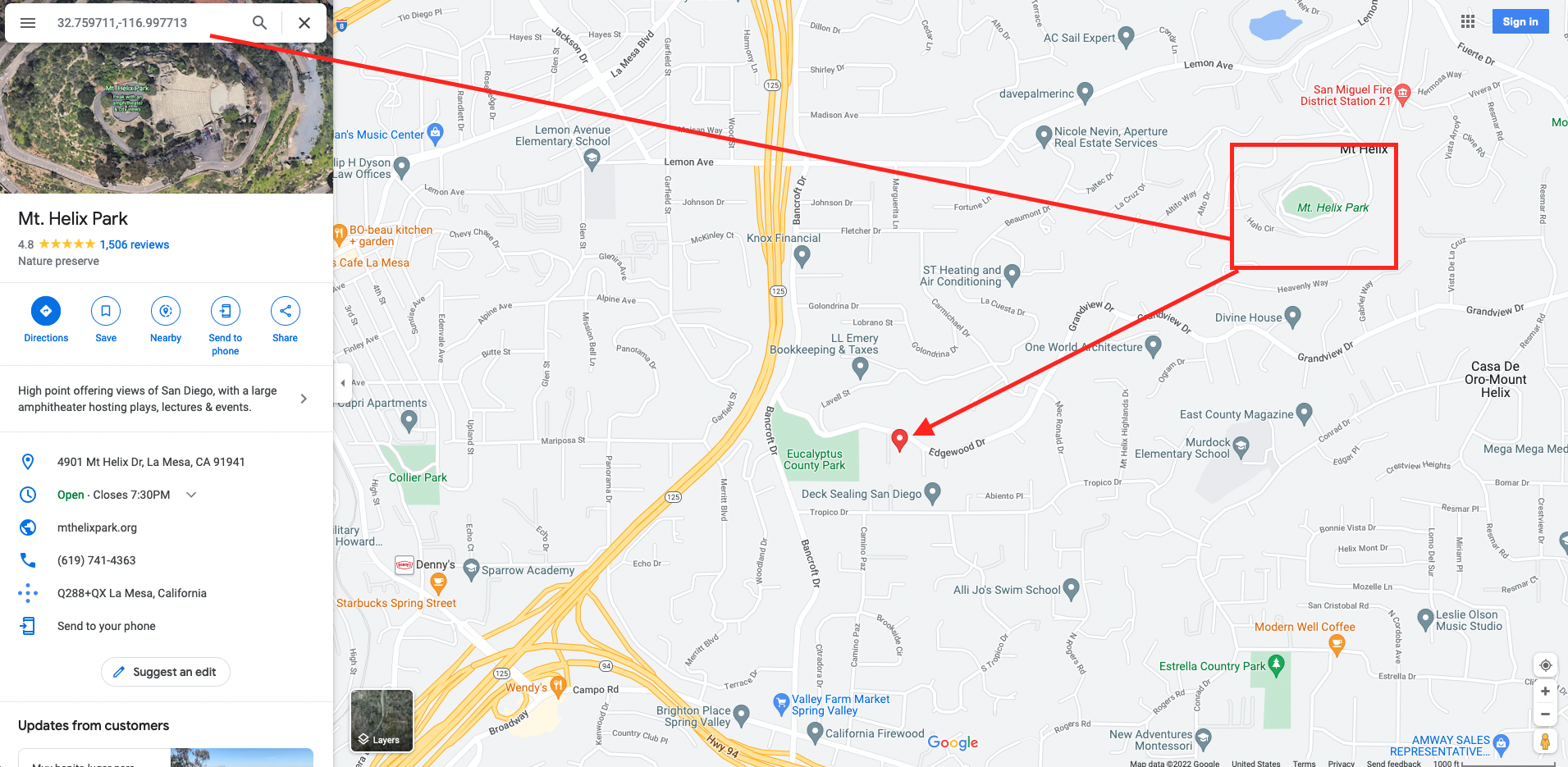
Errors in Geocode Output
Location
- Given: in most spatial data analysis, no choice in location
- No sampling in the usual sense
- Data = attributes augmented with locational information
Spatial Effects
The Trilogy
- Spatial Dependence
- Spatial Heterogeneity
- Spatial Scale
Spatial Dependence
Tobler’s First Law of Geography
“everything depends on everything else, but closer things more so”
- Structure of spatial dependence
- Distance Decay
- Closeness = Similarity
Spatial Heterogenety
Spatial Instability
- Process varies in some way over spatial units
- Multiple forms
- Discrete = regimes
- Continuous = expansion method, GWR
- Trade-off
- Spatial homogeneity = stationary process
- Uniqueness = extreme heterogeneity
Spatial Scale
Mismatch
- Spatial scale of the process
- Spatial scale of our measurement
Issues
- points too far apart = miss small distance variation
- area aggregates cannot provide information on individual behavior
- Ecological Fallacy
Modifiable Areal Unit Problem (MAUP)
Aggregation Problem
- special case of ecological fallacy
- a million correlation coefficients
Zonation Problem
- size
- arangement
- How many ways could you partition the coterminous US land area into 48 polygons?
MAUP Zonation Problem
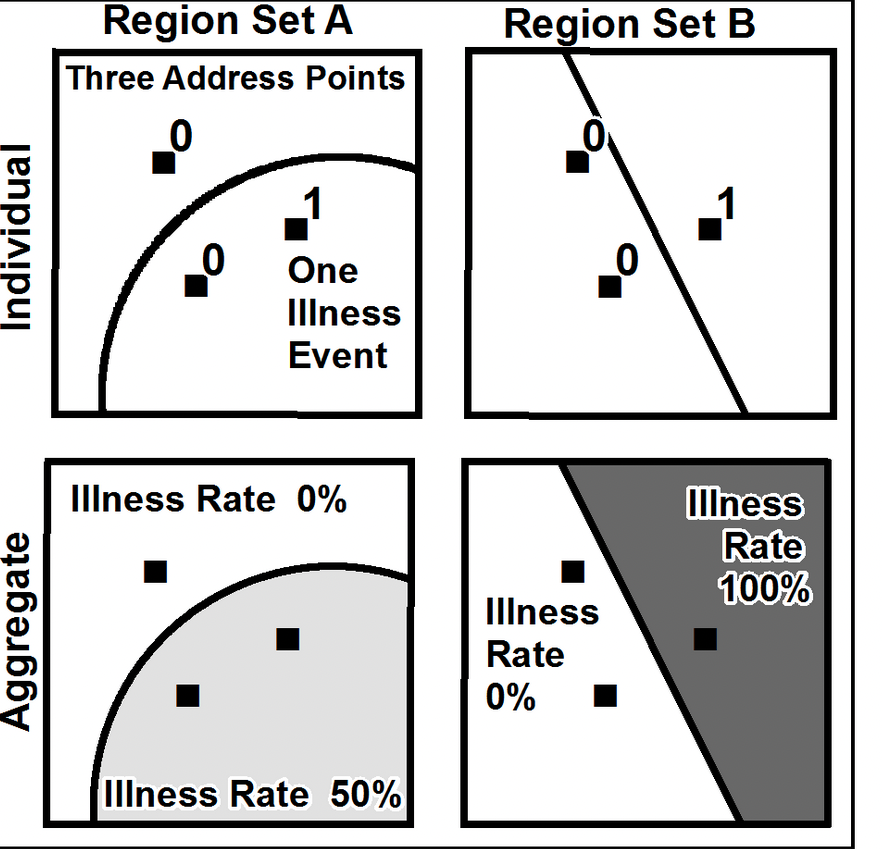
http://en.wikipedia.org/wiki/Modifiable_areal_unit_problem
MAUP Aggregation Problem

- True rate = 1/3 = 33%
- A’s rate = (0 +1/2) /2 = 25%
- A’s weighted rate = 1/3 * 0 + 2/3 * 50 = 33%
- B’s rate = (0 + 100) /2 = 50%
- B’s weighted rate = 2/3 * 0 + 1/3 * 100 = 33%
Types of Spatial Data
Spatial Process
Spatial Random Field
a mathemtical construct to capture randomness of values distributed over space
\[\{Z(s):s \in D \} \]
- \(s \in R^d:\) location (e.g., lat-lon)
- \(D \in R^d:\) index set = possible locations
- \(Z(s):\) random variable at location \(s\)
Types of Spatial Data
Events
- addresses of crimes
Discrete Spatial Objects
- county crime rates
Continuous surfaces
- air quality
- rainfall
Point Pattern Analysis
Data
- mapped pattern = all the values
- not a sample in the usual sense
Spatial Process
- observations as a realization of a random point process
- points occur in space according to a mathematical model
Point Patterns
Unmarked Point Pattern
- only location is recorded
- no other attribute information
Marked Point Pattern
- Location is recorded
- Stochastic attributes are also recorded
- e.g., sales price at address, DBH of a tree
Point Pattern Analysis: Quadrat Methods
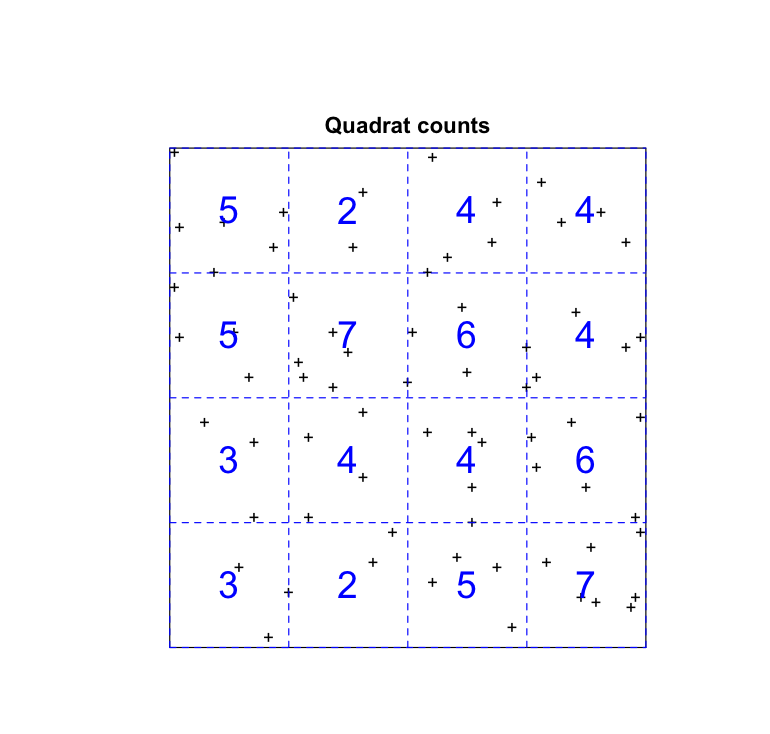
Quadrat Analysis
Point Pattern Analysis: Distance Based Methods
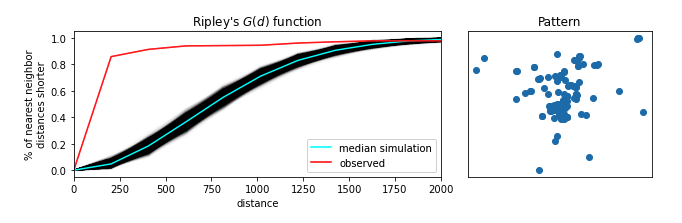
Distance Distributions
Areal Unit Data (Lattice)
Spatial Domain: \(D\)
Discrete and fixed
Locations nonrandom
Locations countable
Examples of lattice data
Attributes collected by ZIP code
census tract
Lattice Data: Indexing
Site
Each location is now an area or site
One observation on \(Z\) for each site
Need a spatial index: \(Z(s_i)\)
\(Z(s_i)\)
\(s_i\) is a representative location within the site
e.g., centroid, largest city
Allows for measuring distances between sites
Lattice Data: County Per Capita Incomes
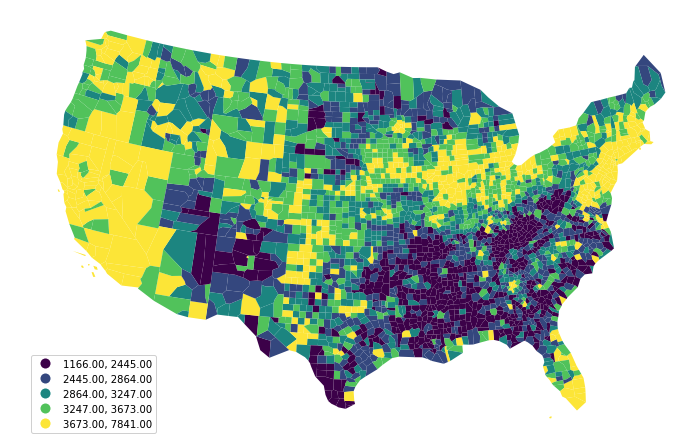
1969
Geostatistical Analysis
Spatial Domain: \(D\)
A continuous and fixed set.
Meaning \(Z(s)\) can be observed everywhere within \(D\).
Between any two sample locations \(s_i\) and \(s_j\) you can theoretically place an infinite number of other samples.
By fixed: the points in \(D\) are non-stochastic
Geostatistical Data
Continuous Variation
Because of the continuity of \(D\)
Geostatistical data is referred to as “spatial data with continuous variation.”
Continuity is associated with \(D\).
Attribute \(Z\) may, or may not, be continuous.
Geostatistical Data: Monitoring Sites
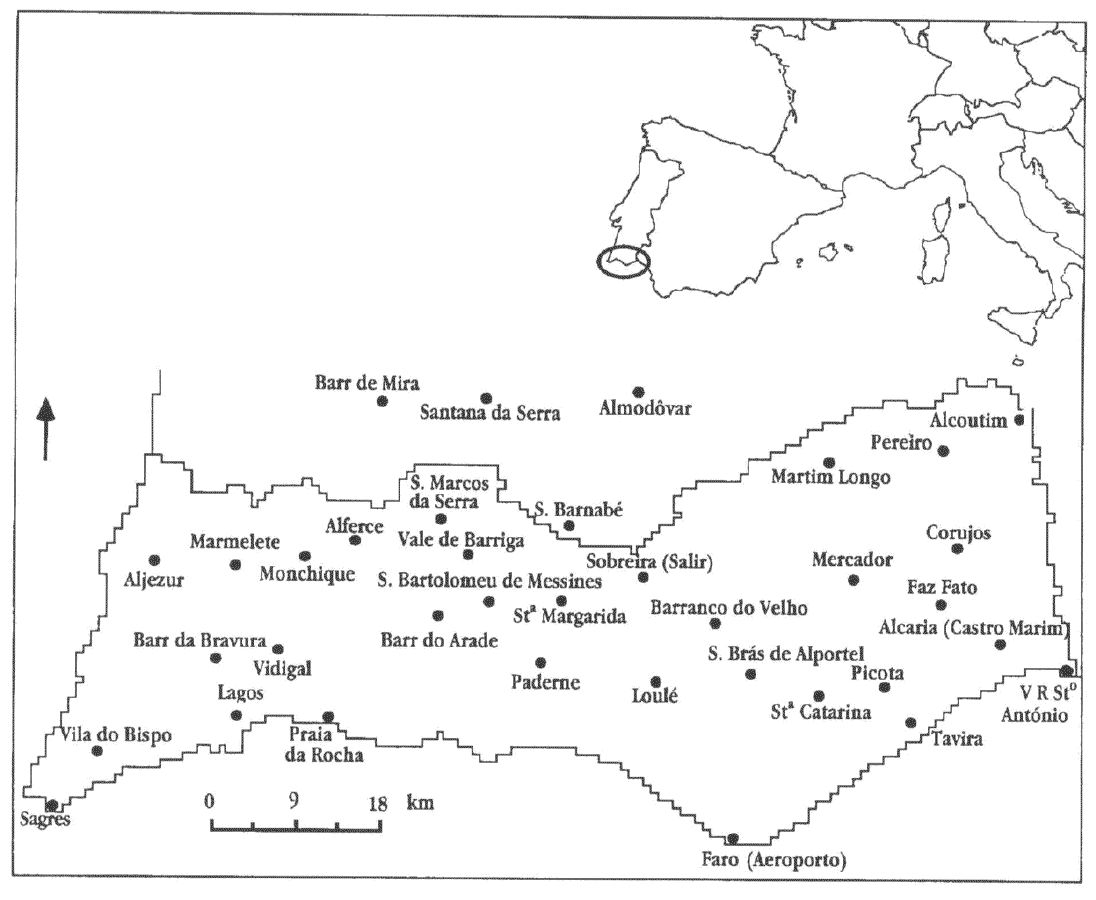
Sites
Geostatistical Data: Surface Reconstruction
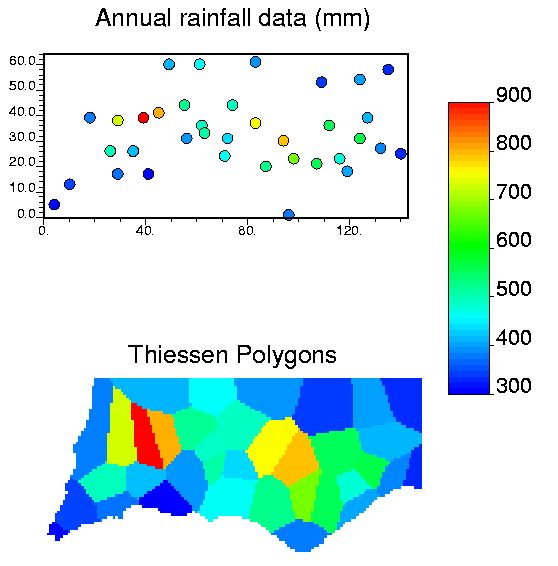
Tessellation
Geostatistical Data: Surface Reconstruction
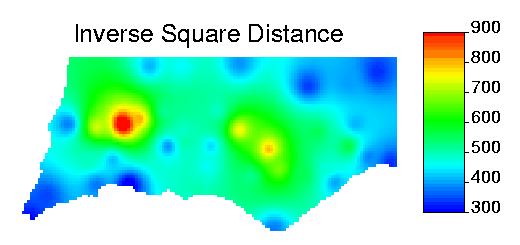
Interpolation
Geostatistical Data: Surface Reconstruction
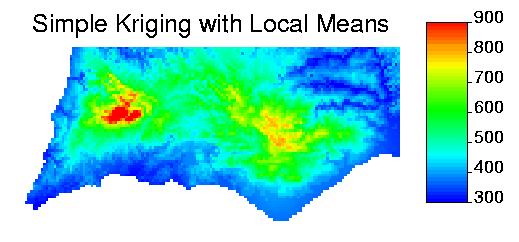
Kriging
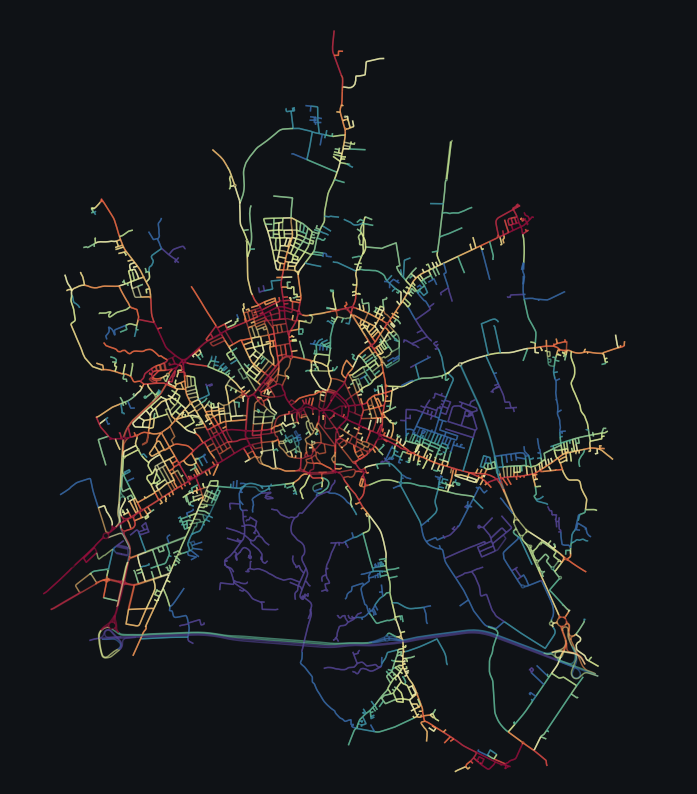
Network Data
A network is a system of linear features connected at intersections and interchanges.
These intersections and interchanges are called nodes.
The linear feature connecting any given pair of nodes is called an arc.
Formally, a network is defined as a directed graph \(G = (N, A)\) consisting of an indexed set of nodes \(N\) with \(n = |N|\) and a spanning set of directed arcs \(A\) with \(m = |A|\), where \(n\) is the number of nodes and \(m\) is the number of arcs.
Each arc on a network is represented as an ordered pair of nodes, in the form from node \(i\) to node \(j\), denoted by \((i, j)\).
Network Data
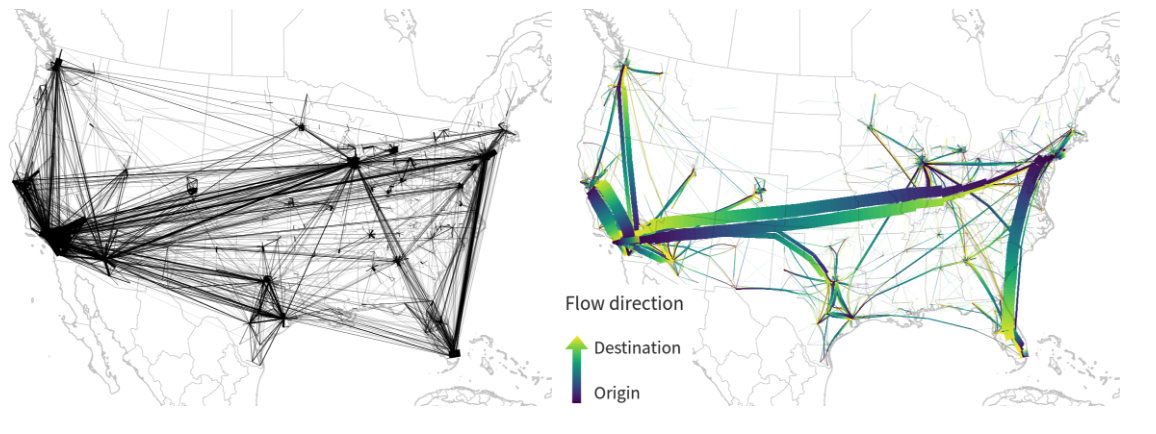
Flow Data
Next Up
Point Pattern Basics